Read this What Is The Difference Between A Parallelogram And A Trapezoid article to find useful information for you, all summarized well by us.

Parallelograms vs. Trapezoids: Distinguishing Two Geometric Shapes
In the fascinating world of geometry, parallelograms and trapezoids hold their own unique places, often inviting confusion due to their shared characteristics. While both possess four sides, our journey will delve into the nuances that set them apart, uncovering their distinctive features and uncovering the secrets that lie within their geometric realms.
Parallelograms: A Balance of Symmetry
A parallelogram, as its name suggests, is a quadrilateral where each pair of opposite sides runs parallel. This inherent parallelism bestows upon parallelograms a unique symmetry, ensuring that their corresponding angles are equal. This equilibrium grants parallelograms their distinctive shape, a harmonious blend of rectangular and diamond-like qualities. Furthermore, the diagonals of a parallelogram bisect each other, forming a captivating intersection at the heart of the shape.
Trapezoids: A Tale of Two Parallel Lines
Unlike parallelograms, trapezoids possess only one pair of parallel sides. This asymmetry adds a dynamic element to their form, breaking away from the perfect symmetry of parallelograms. Trapezoids are often characterized by their two parallel bases and two non-parallel sides, which may take on various angles. This versatility lends trapezoids a wider range of shapes, from isosceles to scalene variations.
Delving into the Historical and Conceptual Nuances
Parallelograms: A Legacy of Ancient Greece
The concept of parallelograms traces its roots back to the dawn of mathematics in ancient Greece. The renowned mathematician Euclid, in his seminal work “Elements,” meticulously defined and explored the properties of parallelograms, laying the foundation for our modern understanding. Parallelograms have since played a pivotal role in various fields, including architecture, engineering, and art.
Trapezoids: A Journey from Pyramids to Calculus
Trapezoids, too, have a rich history, dating back to the enigmatic world of ancient Egypt. Egyptian mathematicians employed trapezoids to calculate the areas of complex shapes, a technique still used today in the famous “trapezoidal rule” of integral calculus. Trapezoids continue to find applications in diverse fields, including geography, physics, and even computer graphics.
Applications: Where Parallelograms and Trapezoids Shine
Parallelograms in the Real World
Parallelograms permeate our surroundings, from the pages of our notebooks to the foundations of our buildings. Their inherent symmetry makes them ideal for creating patterns, tiling surfaces, and designing structures that require strength and stability. Notable examples include the Great Pyramid of Giza, where parallelograms form the base, and the honeycomb patterns found in nature.
Trapezoids in Practice
Trapezoids, with their diverse shapes, serve a multitude of purposes. They form the basis of trapezoidal roofs, which are commonly found in residential and commercial buildings. In physics, trapezoids help us understand the principles of buoyancy and the forces acting on objects in motion. Moreover, trapezoids play a crucial role in computer graphics, where they are used to create smooth curves and transitions.
Trending Topics and Expert Insights
Parallelograms and Vector Analysis
In the realm of vector analysis, parallelograms hold a special significance. The parallelogram law of vector addition states that the sum of two vectors can be represented as a diagonal of a parallelogram with the vectors as its sides. This concept is fundamental to understanding vector operations and their applications in physics and engineering.
Trapezoids in Image Processing
Trapezoids have gained prominence in the field of image processing. They are used to define regions of interest in images, allowing for targeted image analysis and manipulation. Additionally, trapezoids help in perspective transformation, a technique used to correct image distortions caused by camera angles.
Tips and Expert Advice for a Deeper Understanding
Understanding Quadrilaterals
To grasp parallelograms and trapezoids effectively, it’s essential to have a solid foundation in the broader category of quadrilaterals. Familiarize yourself with the different types of quadrilaterals, such as squares, rectangles, and rhombuses, and their defining characteristics.
Visualization is Key
Visualization is a powerful tool when it comes to grasping geometric concepts. Sketch out parallelograms and trapezoids, experimenting with their different properties and variations. This hands-on approach can greatly enhance your intuition and understanding.
FAQ: Unraveling Common Queries
Q: Can a parallelogram be a trapezoid?
A: No, a parallelogram cannot be a trapezoid because parallelograms have two pairs of parallel sides, while trapezoids have only one.
Q: What is the difference between an isosceles trapezoid and a scalene trapezoid?
A: An isosceles trapezoid has two congruent non-parallel sides, while a scalene trapezoid has all four sides of different lengths.
Conclusion: A Clearer Understanding of Geometric Distinctions
In the tapestry of geometry, parallelograms and trapezoids stand as unique and captivating shapes, each possessing its own set of properties and applications. Through this exploration, we have unveiled the subtle nuances that distinguish these two quadrilaterals, allowing us to appreciate their distinct beauty and significance in the world of mathematics and beyond.
Call to Action:
Are you eager to delve further into the captivating world of geometry? Continue your journey by exploring the fascinating properties of other polygons and their applications in various fields. The world of shapes holds endless wonders, waiting to be discovered by curious minds like yours.
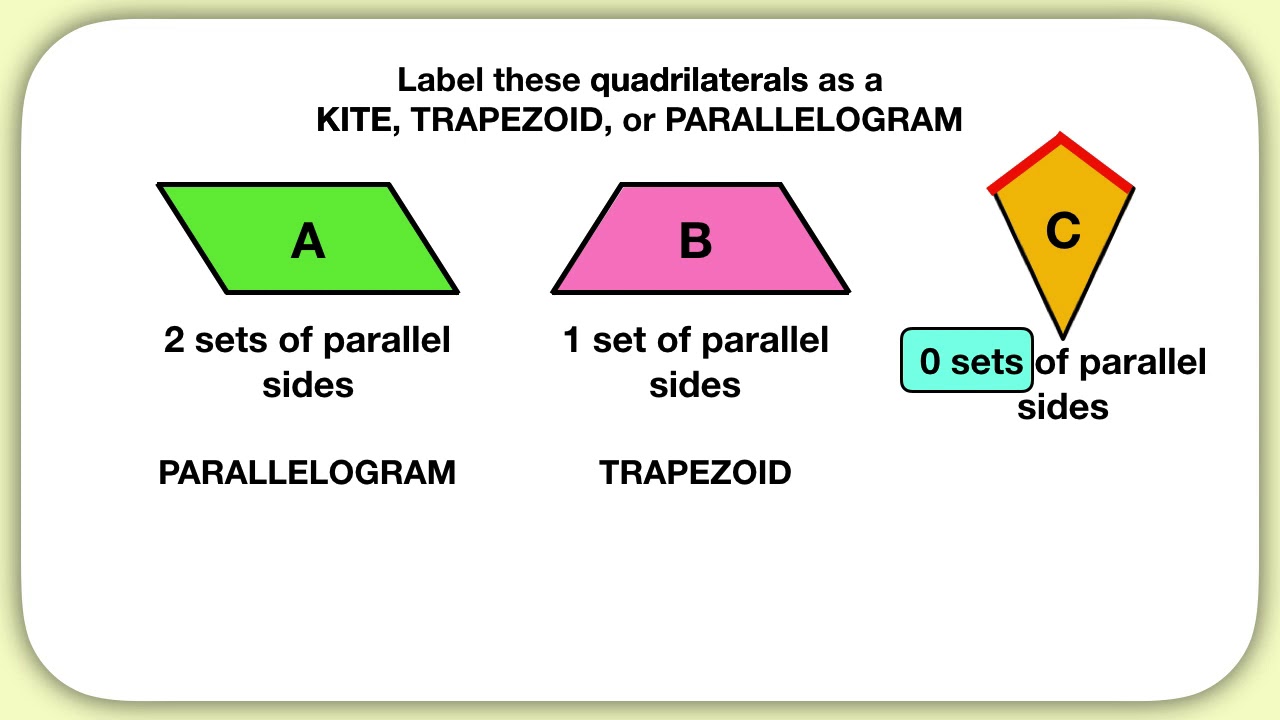
Image: www.youtube.com
An article about What Is The Difference Between A Parallelogram And A Trapezoid has been read by you. Thank you for visiting our website, and we hope this article is beneficial.