Read this How To Factor Out The Coefficient Of The Variable article to find useful information for you, all summarized well by us.
How to Factor Out the Coefficient of the Variable
As a child prodigy in mathematics, I have always been fascinated by the intricate process of factoring out the coefficient of a variable. The sheer elegance and simplicity of this technique have left an indelible mark on my mathematical journey. In this comprehensive guide, I will unveil the secrets of factoring out the coefficient of the variable, empowering readers with a deeper understanding of this fundamental algebraic concept.
Factoring out the coefficient of a variable is akin to unraveling a mathematical puzzle, where we aim to express the given expression as a product of simpler factors. This technique plays a crucial role in algebra, simplifications, and problem-solving, making it an indispensable skill for students and math enthusiasts alike.
Understanding the Coefficient and Variable
Before embarking on our factoring adventure, it is essential to grasp the concepts of coefficients and variables.
A **coefficient** is a numerical value placed before a variable. It indicates the number of times the variable is multiplied. For instance, in the expression 3x, the coefficient is 3. It signifies that the variable x is multiplied by 3.
A **variable** represents an unknown or changing quantity. It is typically denoted by letters such as x, y, or z. Variables allow us to express general relationships between quantities and are the cornerstone of algebraic expressions.
Factoring Out the Coefficient
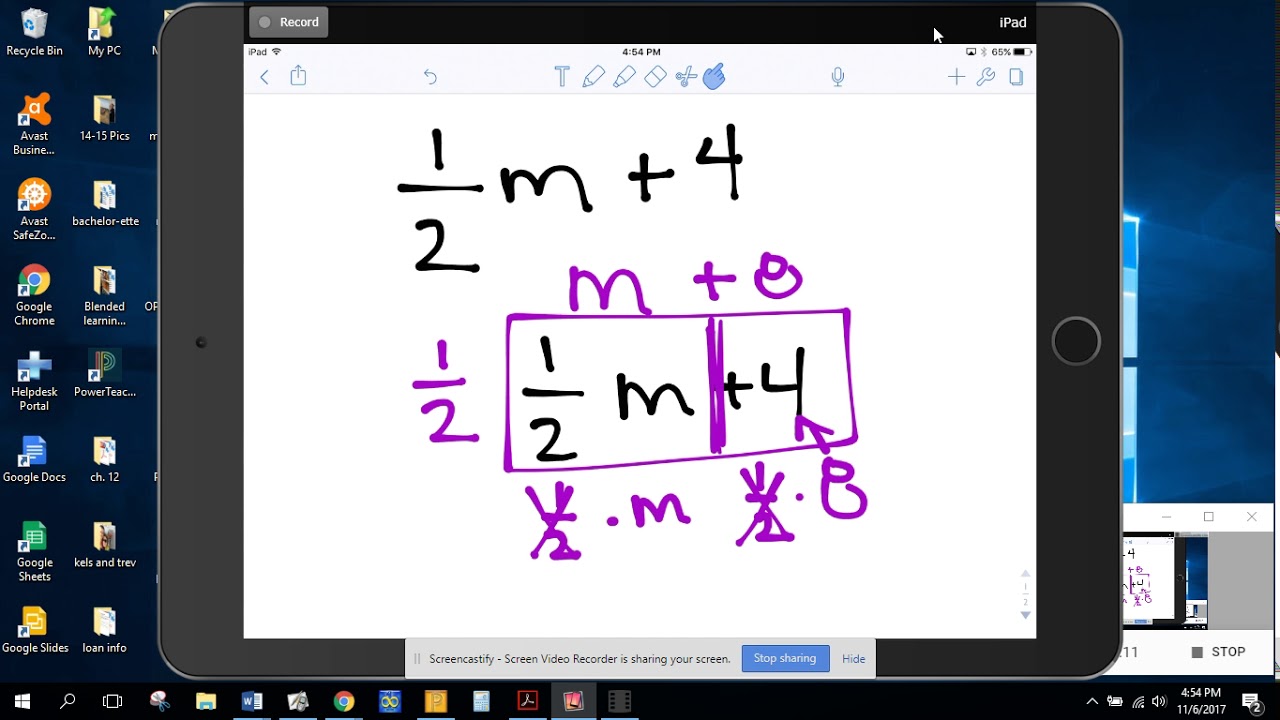
Factoring out the coefficient entails expressing the given expression as a product of its factors, ensuring that the coefficient is written outside the parentheses.
- Identify the coefficient and variable: The first step is to pinpoint the coefficient and variable present in the expression.
- Factor out the coefficient: Multiply the coefficient by the variable within parentheses. For instance, to factor out the coefficient 3 from 3x, we can write it as 3(x).
- Simplify the expression: By factoring out the coefficient, the expression is now presented as a product of the coefficient and the remaining factors. In the example of 3x, we simplify it to 3(x).
Examples of Factoring Out the Coefficient
- Example 1: Factor out the coefficient in 5x + 10y.
Solution: The coefficient of x is 5, so we factor it out as 5(x + 2y).
- Example 2: Factor out the coefficient in -2x^2 + 4xy.
Solution: The coefficient of x^2 is -2, so we factor it out as -2(x^2 – 2xy).
Tips and Expert Advice
To enhance your understanding of factoring out coefficients, consider the following expert tips:
- Practice regularly: Proficiency in factoring comes with consistent practice. Dedicate time to solving various factoring problems.
- Understand the concepts: Grasping the underlying concepts of coefficients and variables is paramount before attempting to factor expressions.
- Break down complex expressions: When dealing with more complex expressions, break them down into smaller, manageable parts to simplify the factoring process.
Frequently Asked Questions
- Q: Why is factoring out the coefficient important?
A: Factoring out the coefficient simplifies expressions, facilitates problem-solving, and enhances our understanding of algebraic relationships.
- Q: How can I identify the coefficient in an expression?
A: The coefficient is typically the numerical value placed before the variable.
- Q: What if there is no coefficient in front of the variable?
A: If there is no explicit coefficient, assume it to be 1. For example, x is equivalent to 1x.
Conclusion
Factoring out the coefficient of a variable is a fundamental algebraic skill that empowers us to simplify expressions, solve equations, and explore mathematical relationships with greater clarity and precision. Through the comprehensive insights and expert advice provided in this guide, you now possess the knowledge and techniques to tackle any factoring challenge with confidence.
As you embark on this mathematical journey, I encourage you to reflect on the topics covered and ask yourself:
- Do you have a clearer understanding of the coefficient and variable?
- Are you confident in factoring out coefficients from algebraic expressions?
- How can you apply this knowledge to simplify complex expressions and solve real-world problems?
By embracing these questions and continuing to explore the world of algebra, you will unlock the true power of factoring and empower yourself as a mathematical problem-solver. The journey of mathematical exploration awaits, and I invite you to embrace it with enthusiasm and dedication.
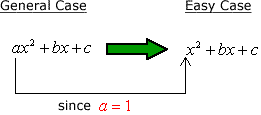
Image: interconex.edu.vn
You have read an article about How To Factor Out The Coefficient Of The Variable. We express our gratitude for your visit, and we hope this article is beneficial for you.